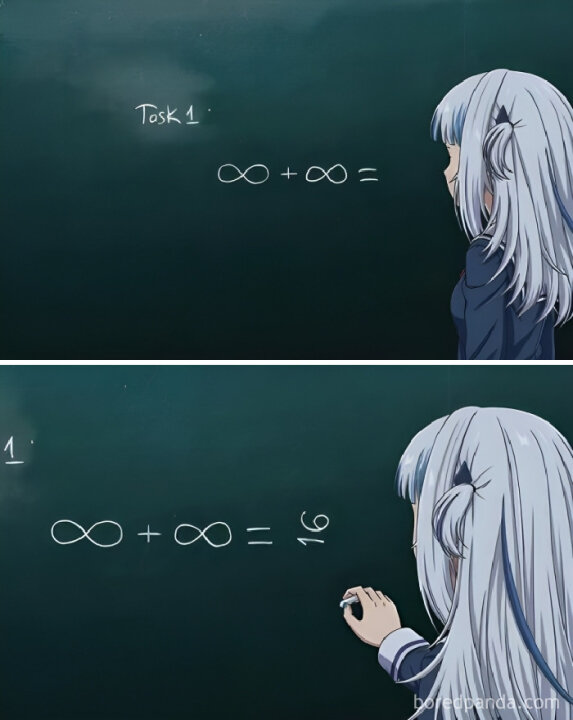It’s simple math.

@crownedwithlaurel97 pretty sure it's an infinity. Though infinity is more of a concept? rather than a number sooooo idk

@pride49 Yep, infinity isn't a number; it's more like a name for the zone beyond everything else. Therefore 2*{infinity}={infinity}.

Math actually has notions of more than one kind of infinity. The first kind, denoted 'aleph zero' involves a one-to-one pairing (mapping) with the counting numbers.

For example, consider multiples of 10. There's 10, 20, 30, 40, ...

There is an easy one-to-one pairing with the counting numbers that goes on for ever. So the counting numbers and the multiples of ten are the same kind of infinity, fit in equivalent infinite sets, whatever. One set is 10x sparser than the other, but they are the same infinity. Weird, I know. Infinity is not a number.

Consider now the real number line which is continuous. There are proofs (Cantor diagonalization) showing that no such mapping exists between counting numbers and reals. So the reals form a different kind of infinity denoted 'aleph one.' I've heard there are higher 'alephs' but I have no idea how to approach them.

@ElwoodBlues sounds irrational to me xD

@crownedwithlaurel97 There is a great documentary on Netflix, or maybe Britbox about infinity, fascinating!