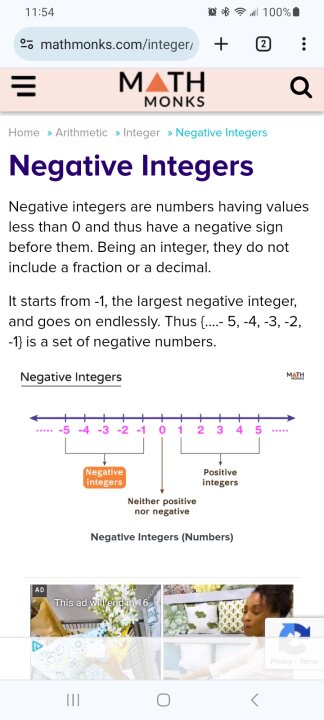
zero plus zero equals zero zero minus zero equals zero zero times zero equals zero
zero isn't really the smallest number, it's the empty number, null, nothing. If it was simply a small number, even the smallest number, than zero + zero > zero. But it isn't.
@Luke73You have it backwards. mathematics has to do with numbers; numbers exists with or without mathematics. Mathematicians didn't even assign names to the number of fingers below. Those symbols and words evolved with languages.
@Luke73 Now that's a more difficult question to answer than that zero thing :) So give me a while to wrap my arms around it. I have a benchmark reference gained from others. Simple, eloquent yet broad. But it wasn't about mathematics.
That is, to define the set, start with an element X(0), then for each n, add a new element X(n) > max { X(m) | m < n }
Then label X(0) with the word, "zero."
Of course, this is sort of circular, since the indices are natural numbers and we assume they have an ordering.
Another approach might be to take an element x, and label it zero. Then make the set { x, {x} }, and call it one. Make the set { x , {x} , { x , {x} } } and call it 2. And so on.
As you go, you let n be the set { x , {x} , , ..., { x , {x} } , ... } }, which has n elements.
Then you define the linear ordering of the labels using set containment of these sets. 0 is in 1 is in 2 is in .... is in n.
The element x is in all sets, so its label zero is the smallest number. Furthemore, a label is a superset of its predecessor label's set, and a subset of its successor label's set.
Note we did not need to know what these labels were geometrically or numerically. The element x was undefined. But the set containment relation defines the linear ordering.
My second definition did not come out of my head, since I had seen something like this before.
Afterward, I looked at Wikipedia and found pretty much the same idea, except the object x was set equal to the empty set. That is better since by definition the empty set is contained in all sets.
I feel so smart now, or at least am pleased with my memory!
@Luke73 I never learned any of this because I hardly ever showed up to school, that’s why I’m asking you lol I never even knew there were unnatural numbers.
@NativePortlander1970 Integers including negative numbers aren't natural numbers. Natural numbers are considered either non-negative integers or positive integers.
@allygator18 I'm aware that there are two definitions but in neither case you prove that 1 or 0 is the smallest, you just assume it. That was the point of this point.
