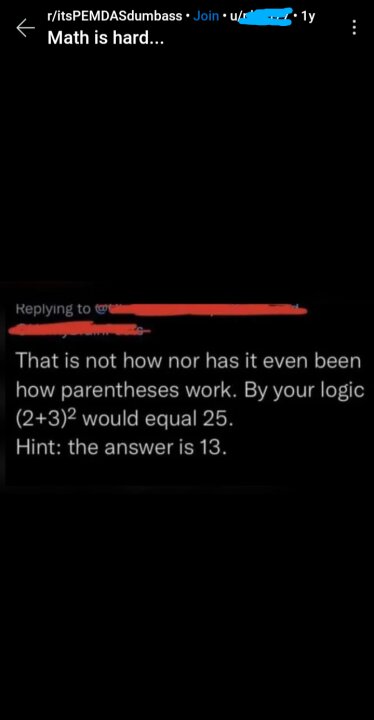
It is NOT 13. 🤣

Saw this post on Reddit before. It's from someone else that took a screenshot of the equation and posted in a subcategory. Many were laughing hard, and some took it seriously.

This page is a permanent link to the reply below and its nested replies. See all post replies »

ScarletWitch · 31-35, F

I thought 6 to the 6th power was 36. I can't remember tbh

xSiFiGamer2016x · 26-30, M

@ScarletWitch Want me to explain? I can help.

SomeMichGuy · M

@ScarletWitch 6^6 means

6*6*6*6*6*6
= (6^2)^3
= (36) * (36) * (36)
= 46,656

xSiFiGamer2016x · 26-30, M

@SomeMichGuy Damn, I was gonna explain it. Oh well. 🤣

SomeMichGuy · M

@xSiFiGamer2016x Show the binomial theorem (how to generate the coefficients of Pascal's triangle)...relevant to the original problem.

xSiFiGamer2016x · 26-30, M

@SomeMichGuy As far as I can remember, this is what I was thinking:

(2+3)² = (2+3)(2+3)

Then did the F.O.I.L. method:

(2+3)(2+3) = 4+6+6+9 = 25

SomeMichGuy · M

@xSiFiGamer2016x Yes

(a + b)^2 = a^2 + 2ab + b^2

(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3

(a + b)^4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4

...

If memory serves, the generalization is:

(a + b)^n = Σ_{j = 0}^{n} (n!/[j!(n-j)!]) a^{n-j}b^{j}

(the binomial theorem).

xSiFiGamer2016x · 26-30, M

@SomeMichGuy

(a + b)^2 = a^2 + 2ab + b^2

I had to write that out, and I still got the answer right. It's been a while since I last used the formula, let alone other theorems.

pawsly · 18-21, F

@SomeMichGuy how's that called generalization it doesn't generalize anything -_- I hate math

SomeMichGuy · M

@xSiFiGamer2016x Good job!

SomeMichGuy · M

@pawsly The binomial theorem gives one the ability to calculate

(a + b)^n

for any n, as a series of n + 1 terms.

So it generalizes the specific examples to any n.

Or you can write out Pascal's triangle...do it to n = 20...lmao.

The formula is obviously a generalization, and makes having a bunch of specific examples unnecessary.