This page is a permanent link to the reply below and its nested replies. See all post replies »

SW-User
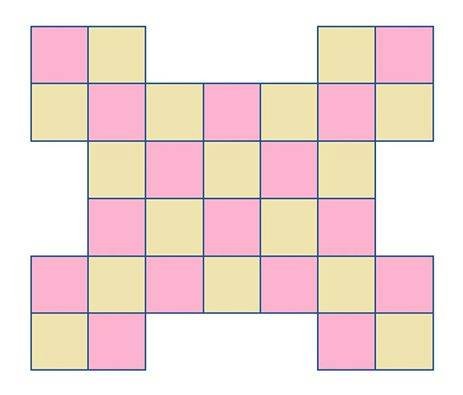
88. @PirateMonkeyCabinet explained all the blue outlines, but forgot the yellow and pink filled ones.

SW-User
@SW-User 88 is the wrong answer.

SW-User
@SW-User Are you sure? To be more specific: would you consider changing the best answer if I can prove there are more than 56? My calculation was fairly quick, so I'm not convinced there are 88, but if you make it worth for me to create a gif, I'll give it a chance.
PirateMonkeyCabinet · 36-40, M
@SW-User Technically, you aren't necessarily wrong, but I also don't entirely agree. By all means, if someone has a better answer than me then they deserve to get the best answer. However, this becomes a matter of definition.
If I understand you correctly, you want to define the borders (the blue lines) as separate entities from the fill color within. Thus getting a double count for the squares; once for the border, once for the fill. Again, technically this isn't necessarily wrong but it depends on the definition of the task and what its intended boundaries are.
There are multiple potential definitions which support the answer being 56:
* Consider the border part of each square, so that each fill color + border equals one combined unit, or one square.
* Consider the border a readability enhancer - with the intention of making it clearer where one base square ends and a new one begins - and therefore not count it as part of the squares themselves. Almost as if each colored square is a cardboard box and the lines we see are just the edges of the boxes being visible to us as we look down on them.
* Consider the fill color itself as a readability enhancer. Trying to count a bunch of identical squares next to each other is a great recipe for losing track of where you are when you are counting your way along it. Having some differentiation makes it easier to not lose your count.
I'd wager that most people would consider it as being implied, written between the lines if you will, that the squares and borders would not be considered separate entities for counting purposes.
But again, you're not technically wrong as it as the condition isn't explicitly stated, so with the right definition your answer would probably be correct. That being said, if we're going to go down the rabbit hole of technically correct definitions, there is a ton of potentially correct answers:
* The intersection point between two lines of equal thickness would also be a square in itself.
* Each pixel is also square (unless you have some specialized monitor, or a monitor from a bygone era), so technically one could also count each pixel, each set of 2x2 pixels, and so on.
* But what if you have a low resolution on your monitor, then each pixel might be relatively large. The task doesn't explicitly state I can't subdivide each pixel, so I could start measuring 1 mm by 1 mm squares.
I could probably think up a ton more definitions that support a multitude of different technically correct answers. I'd still say there is an argument for it that common perceptions of the intended definition and method for solving the task follows one of the three ones I laid out as potential definitions for the answer being 56.
If I understand you correctly, you want to define the borders (the blue lines) as separate entities from the fill color within. Thus getting a double count for the squares; once for the border, once for the fill. Again, technically this isn't necessarily wrong but it depends on the definition of the task and what its intended boundaries are.
There are multiple potential definitions which support the answer being 56:
* Consider the border part of each square, so that each fill color + border equals one combined unit, or one square.
* Consider the border a readability enhancer - with the intention of making it clearer where one base square ends and a new one begins - and therefore not count it as part of the squares themselves. Almost as if each colored square is a cardboard box and the lines we see are just the edges of the boxes being visible to us as we look down on them.
* Consider the fill color itself as a readability enhancer. Trying to count a bunch of identical squares next to each other is a great recipe for losing track of where you are when you are counting your way along it. Having some differentiation makes it easier to not lose your count.
I'd wager that most people would consider it as being implied, written between the lines if you will, that the squares and borders would not be considered separate entities for counting purposes.
But again, you're not technically wrong as it as the condition isn't explicitly stated, so with the right definition your answer would probably be correct. That being said, if we're going to go down the rabbit hole of technically correct definitions, there is a ton of potentially correct answers:
* The intersection point between two lines of equal thickness would also be a square in itself.
* Each pixel is also square (unless you have some specialized monitor, or a monitor from a bygone era), so technically one could also count each pixel, each set of 2x2 pixels, and so on.
* But what if you have a low resolution on your monitor, then each pixel might be relatively large. The task doesn't explicitly state I can't subdivide each pixel, so I could start measuring 1 mm by 1 mm squares.
I could probably think up a ton more definitions that support a multitude of different technically correct answers. I'd still say there is an argument for it that common perceptions of the intended definition and method for solving the task follows one of the three ones I laid out as potential definitions for the answer being 56.

SW-User
@SW-User Interesting. Explain?
Honestly, I can see what you mean. But I don't think it is necessary to point out the extra solution of counting those colorful squares since this question is asking how many squares (it doesn't matter if you separate the line of the square or its colors), and by that means, you count the square (the shape that includes both the line and color), not the line nor colors. You count them as a whole.
But it is impressive to figure out that you can add the blue line or the color as a separate bonus to count the square.
Honestly, I can see what you mean. But I don't think it is necessary to point out the extra solution of counting those colorful squares since this question is asking how many squares (it doesn't matter if you separate the line of the square or its colors), and by that means, you count the square (the shape that includes both the line and color), not the line nor colors. You count them as a whole.
But it is impressive to figure out that you can add the blue line or the color as a separate bonus to count the square.

SW-User
@SW-User both an area and an outline match the definition of a square. As the caption doesn't specify which to count, we should count both.
@PirateMonkeyCabinet you have a point there, but that takes it yet another step further. My interpretation takes a second definition into account, but still only counts the given boundaries. If you take the freedom to add additional boundaries, there is literally an infinite amount depending on how detailed you want to get.
@PirateMonkeyCabinet you have a point there, but that takes it yet another step further. My interpretation takes a second definition into account, but still only counts the given boundaries. If you take the freedom to add additional boundaries, there is literally an infinite amount depending on how detailed you want to get.