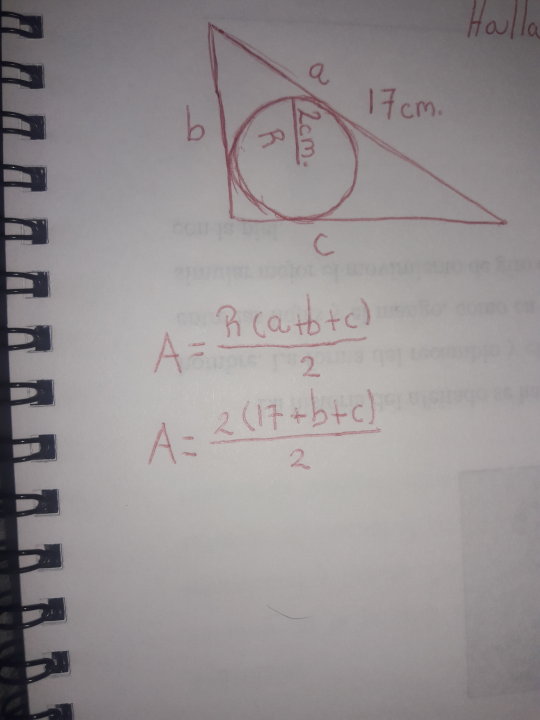This page is a permanent link to the reply below and its nested replies. See all post replies »
dirge · M
What is the perimeter of a right triangle such that the hypotenuse is 17 units and a circle with a radius of 2 is inscribed within the triangle?
This message was deleted by its author.
This message was deleted by its author.
JoyfulSilence · 51-55, M
The answer is 38.
I drew a diagram.
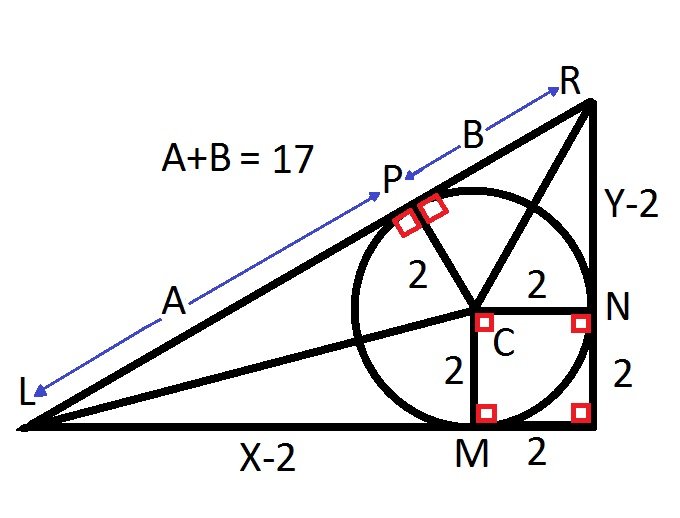
Given this diagram, we have 4 small triangles
1 = P, C, L
2 = M, C, L
3 = P, C, R
4 = N, C, R
Then A+B = distance from L to R, which is 17.
Triangle 1 has legs of length A and 2.
Triangle 2 has legs of length X-2 and 2.
Both have the same hypotenuse.
So A^2 + 4 = (X-2)^2 + 4,
Or X = A + 2
Triangle 3 has legs of length B and 2.
Triangle 4 has legs of length Y-2 and 2.
Both have the same hypotenuse.
So B^2 + 4 = (Y-2)^2 + 4,
Or Y = B + 2
The perimeter is
X + Y + 17
= ( A + 2 ) + ( B + 2 ) + 17
= ( A + B ) + 2 + 2 + 17
= ( A + B ) + 21
= 17 + 21
= 38
QED.
I drew a diagram.

Given this diagram, we have 4 small triangles
1 = P, C, L
2 = M, C, L
3 = P, C, R
4 = N, C, R
Then A+B = distance from L to R, which is 17.
Triangle 1 has legs of length A and 2.
Triangle 2 has legs of length X-2 and 2.
Both have the same hypotenuse.
So A^2 + 4 = (X-2)^2 + 4,
Or X = A + 2
Triangle 3 has legs of length B and 2.
Triangle 4 has legs of length Y-2 and 2.
Both have the same hypotenuse.
So B^2 + 4 = (Y-2)^2 + 4,
Or Y = B + 2
The perimeter is
X + Y + 17
= ( A + 2 ) + ( B + 2 ) + 17
= ( A + B ) + 2 + 2 + 17
= ( A + B ) + 21
= 17 + 21
= 38
QED.
JoyfulSilence · 51-55, M
I edited my reply to fix typos and errors. So you might want to read it again.
AndyC · 22-25, F
@JoyfulSilence I'm reading it... translating it to Spanish and doing the excersice step by step.
JoyfulSilence · 51-55, M
JoyfulSilence · 51-55, M