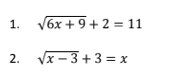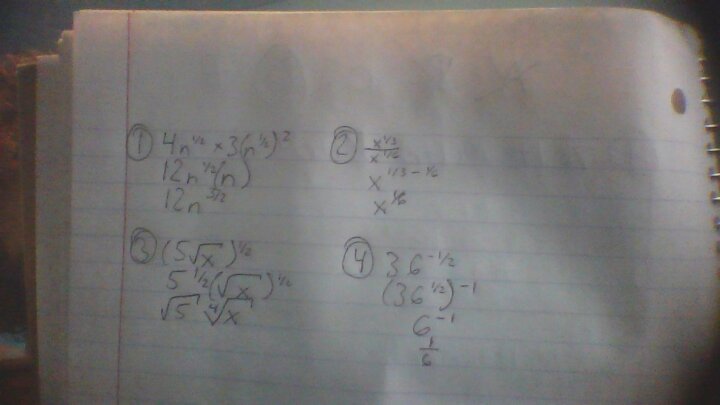
View 2 more replies »
BlueVeins · 22-25
MightyLion · 22-25, M
I am so sorry for making you work so hard I only need the second question of the image that is now up@BlueVeins
MightyLion · 22-25, M
I will give you best answer for your efforts. @BlueVeins
ArishMell · 70-79, M
These are expressions not equations, so with the exception of (4) can only be simplified at best. So those instructions are therefore not applicable here.
I don't know what you mean by "extraneous" solutions but equations with x^(2 and over) can have what are called their "roots", which I think are where y = 0. When plotted as graphs these are the curves' intercepts on the x-axis.
However, if it's any help, and I am stretching what algebra I can recall and understand, I offer these. Sorry - I can't see how to type indices correctly in what's only a basic text-editor.
(1) simplify first to 4√n * 3√n.
That is because the original end n term is the square root of n squared.
I think it then becomes
[12√n√n] = 12n.
'
2) A reciprocal index signifies the root. So the expression is the
[(cube-root of x) / (6th root of x)],
but I'm afraid I'm stuck at that point. It might simplify further but I can't see how.
'
3) I think that is only the square root of [(5√x)] so doesn't really get you anywhere. You may as well just replace the index at the end with a square-root sign at the front.
'
4) This one does simplify to a number because the index is working on a definite value; and one with a nice simple root. The index (1/2) means the square root. Making the index negative means the root's reciprocal. So:
[36^(- 1/2)] = [1/(√36)] = 1/6 = 0.1666 recurring.
(I had to verify this by calculator.... )
I don't know what you mean by "extraneous" solutions but equations with x^(2 and over) can have what are called their "roots", which I think are where y = 0. When plotted as graphs these are the curves' intercepts on the x-axis.
However, if it's any help, and I am stretching what algebra I can recall and understand, I offer these. Sorry - I can't see how to type indices correctly in what's only a basic text-editor.
(1) simplify first to 4√n * 3√n.
That is because the original end n term is the square root of n squared.
I think it then becomes
[12√n√n] = 12n.
'
2) A reciprocal index signifies the root. So the expression is the
[(cube-root of x) / (6th root of x)],
but I'm afraid I'm stuck at that point. It might simplify further but I can't see how.
'
3) I think that is only the square root of [(5√x)] so doesn't really get you anywhere. You may as well just replace the index at the end with a square-root sign at the front.
'
4) This one does simplify to a number because the index is working on a definite value; and one with a nice simple root. The index (1/2) means the square root. Making the index negative means the root's reciprocal. So:
[36^(- 1/2)] = [1/(√36)] = 1/6 = 0.1666 recurring.
(I had to verify this by calculator.... )
MightyLion · 22-25, M
I'm not sure how correct you are but I hearted it for effort and thank you. @ArishMell
ArishMell · 70-79, M
@MightyLion Thank you! You'e not sure how correct I am... That's handy!
I tried the two equations you posted later but though their first was simple the other defeated me completely.
I tried the two equations you posted later but though their first was simple the other defeated me completely.
ArishMell · 70-79, M
Having had half of SW puzzling over a set of unrelated expressions...
It's not easy doing maths on a plain text-editor either, because it does not allow you to type the indices etc properly.
(1) becomes 6x+9 = 81 (11-2 = 9 on RHS, then square both sides)
so 6x = 81-9
x = 12.
(2) That will become a regular quadratic equation if we re-arrange and square through.
sqrt(x-3) = x-3
x-3 = (x-3)^2.
I've a feeling I'm over-thinking this one. Though an equation so LHS=RHS, it is the sort that has a false air of symmetry to make you think you are missing something really obvious and simple, solvable mentally in two or three steps...!
x-3 = x^2-6x+9
I had to expand the expression by long-multiplication on paper as I could not remember how to do it mentally. It doesn't look right though. It seems too complicated, especially as the next step reveals a prime number in it:
x^2-7x = -12.
Or x^2-7x+12 = 0.
No. I'll have to admit defeat there I'm afraid. There is a rather long-winded formula for solving equations like that but I can't remember it, would struggle to find it and anyway I think I have gone completely wrong. Maths exercise questions tend to be designed to shake out quite neatly, like No.1 above, because it's practicing the technique that matters.
Oh well, fun trying......
It's not easy doing maths on a plain text-editor either, because it does not allow you to type the indices etc properly.
(1) becomes 6x+9 = 81 (11-2 = 9 on RHS, then square both sides)
so 6x = 81-9
x = 12.
(2) That will become a regular quadratic equation if we re-arrange and square through.
sqrt(x-3) = x-3
x-3 = (x-3)^2.
I've a feeling I'm over-thinking this one. Though an equation so LHS=RHS, it is the sort that has a false air of symmetry to make you think you are missing something really obvious and simple, solvable mentally in two or three steps...!
x-3 = x^2-6x+9
I had to expand the expression by long-multiplication on paper as I could not remember how to do it mentally. It doesn't look right though. It seems too complicated, especially as the next step reveals a prime number in it:
x^2-7x = -12.
Or x^2-7x+12 = 0.
No. I'll have to admit defeat there I'm afraid. There is a rather long-winded formula for solving equations like that but I can't remember it, would struggle to find it and anyway I think I have gone completely wrong. Maths exercise questions tend to be designed to shake out quite neatly, like No.1 above, because it's practicing the technique that matters.
Oh well, fun trying......
DrWatson · 70-79, M
There are no equations here, just radical expressions. If the instructions talk of squaring both sides, then you must be posting the wrong thing, because there are no equal signs, and thus we do not have two "sides".
JimboSaturn · 56-60, M
@DrWatson I think the instructor should be asking to simplify.
MightyLion · 22-25, M
I put the wrong image twice, you might have to refresh the page to see the right image which only has two questions. @JimboSaturn
DrWatson · 70-79, M
@JimboSaturn Yes, but he put the wrong image up.
Mamapolo2016 · F
Sorry. All I know to do about radical equations is to put up sawhorses, wear riot gear, and hope they go away.
JimboSaturn · 56-60, M
I could but I'm too lazy and apathetic :P
What language are you speaking?