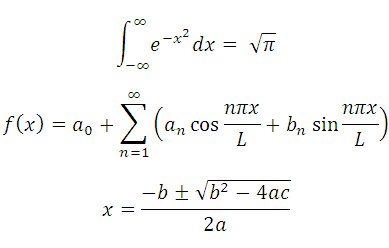This page is a permanent link to the reply below and its nested replies. See all post replies »
SomeMichGuy · M
@Biffed No, but you likely saw the last one in high school if you took algebra; it is the "quadratic formula", which gives the solutions to the "quadratic equation"
a(x^2) + bx + c = 0
("Quadratic" means "squared"/"second order"--the highest power of x is 2, so it's a quadratic equation.)
The second one shows a full Fourier representation of a function f(x) defined on a characteristic interval
0 <= x <= L. This special "expansion" is called a "Fourier series", and it shows how a function can be broken down into a constant (a_0) and a set of "even" (cosine) and "odd" (sine) components. Finding them is done by using calculus (integration) and the properties of these functions.
The first formula expresses normalization of the "normal" or "Gaussian" distribution‐‐AKA "the Bell curve". (By "substitution of variables", you can easily extend this to the more typical
e^(‐k[x^2]) for k other than 1.)
a(x^2) + bx + c = 0
("Quadratic" means "squared"/"second order"--the highest power of x is 2, so it's a quadratic equation.)
The second one shows a full Fourier representation of a function f(x) defined on a characteristic interval
0 <= x <= L. This special "expansion" is called a "Fourier series", and it shows how a function can be broken down into a constant (a_0) and a set of "even" (cosine) and "odd" (sine) components. Finding them is done by using calculus (integration) and the properties of these functions.
The first formula expresses normalization of the "normal" or "Gaussian" distribution‐‐AKA "the Bell curve". (By "substitution of variables", you can easily extend this to the more typical
e^(‐k[x^2]) for k other than 1.)
